Bootstrapping a Poisson GLMM with glmmBoot

Last updated on May 28, 2020 Bootstrap, GLMM, R

This code to illustrates the implementation of the bootstrapping methods described in (Flores-Agreda and Cantoni, Under Review) in a real-data context. Data comes from the example found in Molenberghs & Verbeke (2006) initially reported by Faught et. al. (1996).

Analysis

To start performing the analysis, you need:

  1. the following packages:
library(lme4)
library(glmmTMB)
library(sas7bdat)
library(TMB)
library(dplyr)
library(ggplot2)
  1. to compile glmm_rirs.cpp and load the resulting binary into the environment:
compile(file = "glmmBoot/src/glmm_rirs.cpp")
dyn.load(dynlib("glmmBoot/src/glmm_rirs"))
  1. the functions in the file glmmBoot.R:
source("glmmBoot/R/glmmBoot.R")
  1. the dataset epilepsy.sas7bdat
epilepsy <- read.sas7bdat(file = "glmmBoot/data/epilepsy.sas7bdat")

Model

The aim of the study was to verify the effects of an new anti-epileptic drug (AED) compared to a placebo on the number of seizures experienced by patients during the study. To do this, consider a mixed Poisson model for the outcome containing two potentially correlated random effects: one for a random intercept and another one for the visit time i.e. \(y_{ij}|\mathbf{u}_i\sim \mathcal{P}(\lambda_{ij})\) with:

\[\log(\lambda_{ij}) = \beta_0 + \beta_{1} T_{ij} + \beta_{2}t_{ij} + \beta_{3} T_{ij}t_{ij} + \sigma_{1} u_{i1} + \sigma_{2} u_{i2} t_{ij}\]

where:

  • \(T_{ij}\) represents the effect of the treatment and
  • \(t_{ij}\) the visit time.

The variance-covariance structure of the vector of Normal random effects \(\mathbf{u}_i = [u_{i1}, u_{i2}]^T\), comprises a correlation coefficient \(\rho\) , i.e.

\[\mathbf{D}(\mathbf{\sigma}) = \left[\begin{array}{c c} \sigma_{1}^2 & \rho\sigma_{1}\sigma_{2} \\ \rho\sigma_{1}\sigma_{2} & \sigma_{2}^2 \end{array}\right].\]

Implementation

estimate_glmm()

The function estimate_glmm() estimates the model with a TMB template using the frame and estimates of objects of class glmerMod as starting values. For example:

obj.glmerMod <- lme4::glmer(nseizw~ trt*studyweek + (studyweek|id), 
                            family = "poisson",
                            data = epilepsy, 
                            control = glmerControl(optimizer = "bobyqa"))

for comparison purposes, let us also extract the estimates of this object

A comparison of the estimates yields:

est_lmer %>% 
  inner_join(est_tmb, by=("Parameters"), suffix=c(" (glmer)", " (TMB)")) %>% 
  kable(digits = 4)
Parameters Estimates (glmer) Std..Errors (glmer) Estimates (TMB) Std..Errors (TMB)
(Intercept) 0.8945 0.1782 0.8945 0.1786
trt -0.2443 0.2538 -0.2443 0.2544
studyweek -0.0271 0.0099 -0.0271 0.0099
trt:studyweek 0.0107 0.0138 0.0107 0.0139
s_1 1.1272 NA 1.1273 0.0975
s_2 0.0487 NA 0.0487 0.0057
rho -0.3339 NA -0.3339 0.1312

The generation of replicates using Random Weighted Laplace Bootstrap (Flores-Agreda and Cantoni, Under Review) is carried by the function bootstrap_glmm(), with the option method=rwlb.

## Bootstrap inference 
rwlb_reps <- bootstrap_glmm(obj.glmerMod,
                            B = 1000,
                            method = "rwlb")

The resulting Bootstrap replicates are stored in an object of the class glmmBoot, which can be used to construct:

  • Estimates of the Parameters: by averaging over the replicates.
  • Estimates of the Standard Errors: by computing the standard deviations for the replicates.
  • Percentile-based and Studentized Confidence Intervals (CI) with a level of 95%.

Methods

confint()

produces bootstrap estimates, standard errors and confidence intervals with the percentile and studentized methods

  • Example of the percentile method
rwlb_reps %>% 
  confint(bootstrap_type = "percentile")%>% 
  kable(digits = 4)
Parameters Estimate Std_Errors ci_lower ci_upper
(Intercept) 0.8890 0.1550 0.5771 1.1726
rho -0.3193 0.1623 -0.6379 -0.0232
s_1 1.1068 0.1288 0.8879 1.3936
s_2 0.0471 0.0073 0.0335 0.0625
studyweek -0.0271 0.0087 -0.0449 -0.0113
trt -0.2372 0.2512 -0.7172 0.2332
trt:studyweek 0.0106 0.0139 -0.0164 0.0375
  • Example of the studentized method
rwlb_reps %>% 
  confint(bootstrap_type = "studentized") %>%
  kable(digits = 4)
Parameters Estimate Std_Errors ci_lower ci_upper
(Intercept) 0.8890 0.1550 0.5820 1.1882
rho -0.3193 0.1623 -0.7402 -0.0651
s_1 1.1068 0.1288 0.8292 1.3248
s_2 0.0471 0.0073 0.0316 0.0601
studyweek -0.0271 0.0087 -0.0446 -0.0099
trt -0.2372 0.2512 -0.7369 0.2429
trt:studyweek 0.0106 0.0139 -0.0163 0.0374

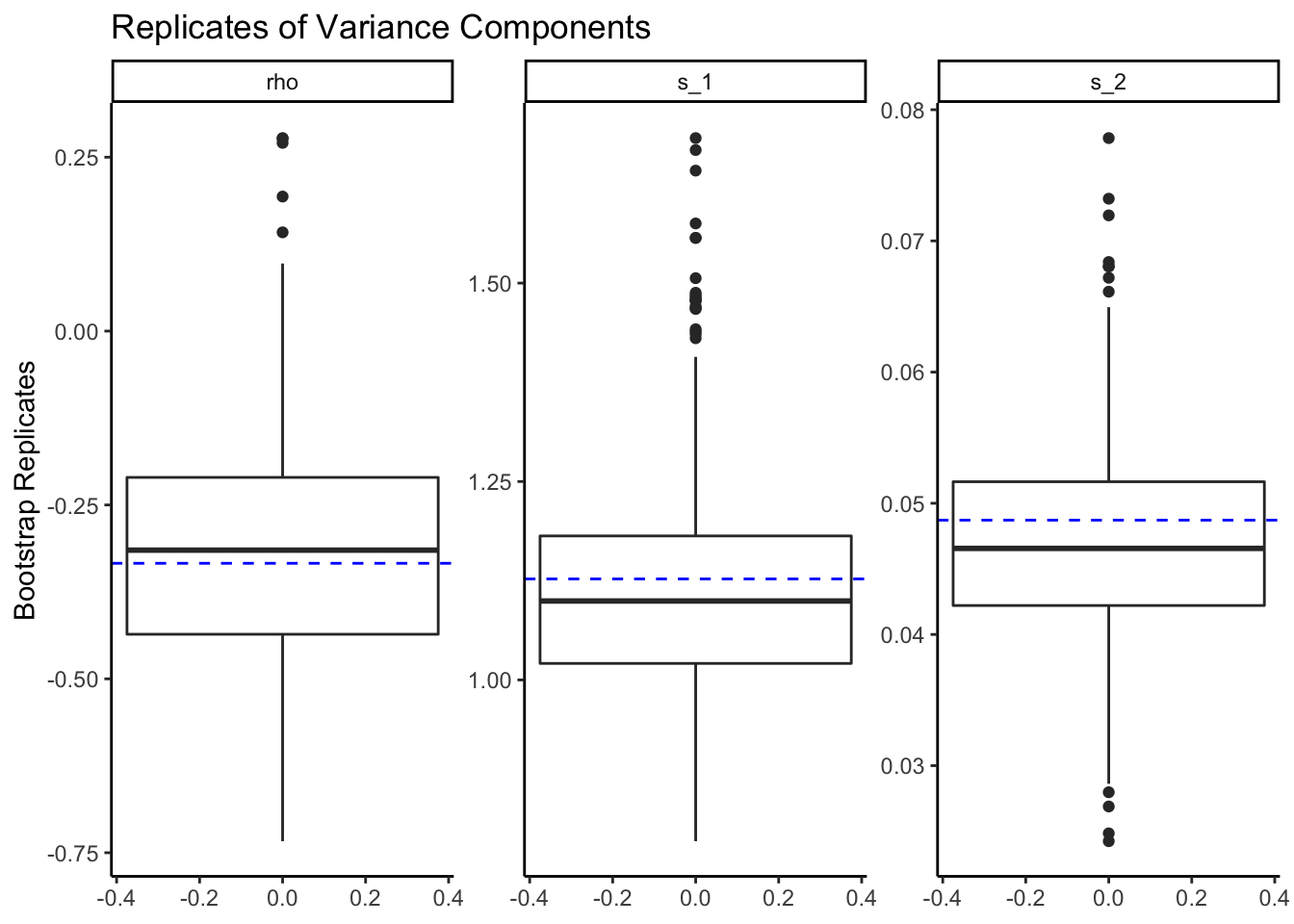
plot()

Shows the boxplots of the replicates for all the parameters or a subset with a line describing the TMB estimates

  • fixed effect parameters
plot(rwlb_reps, 
     parm_subset=c("(Intercept)", "trt", "studyweek", "trt:studyweek")) + 
  ggtitle("Replicates of Fixed Effects") +
  theme_classic()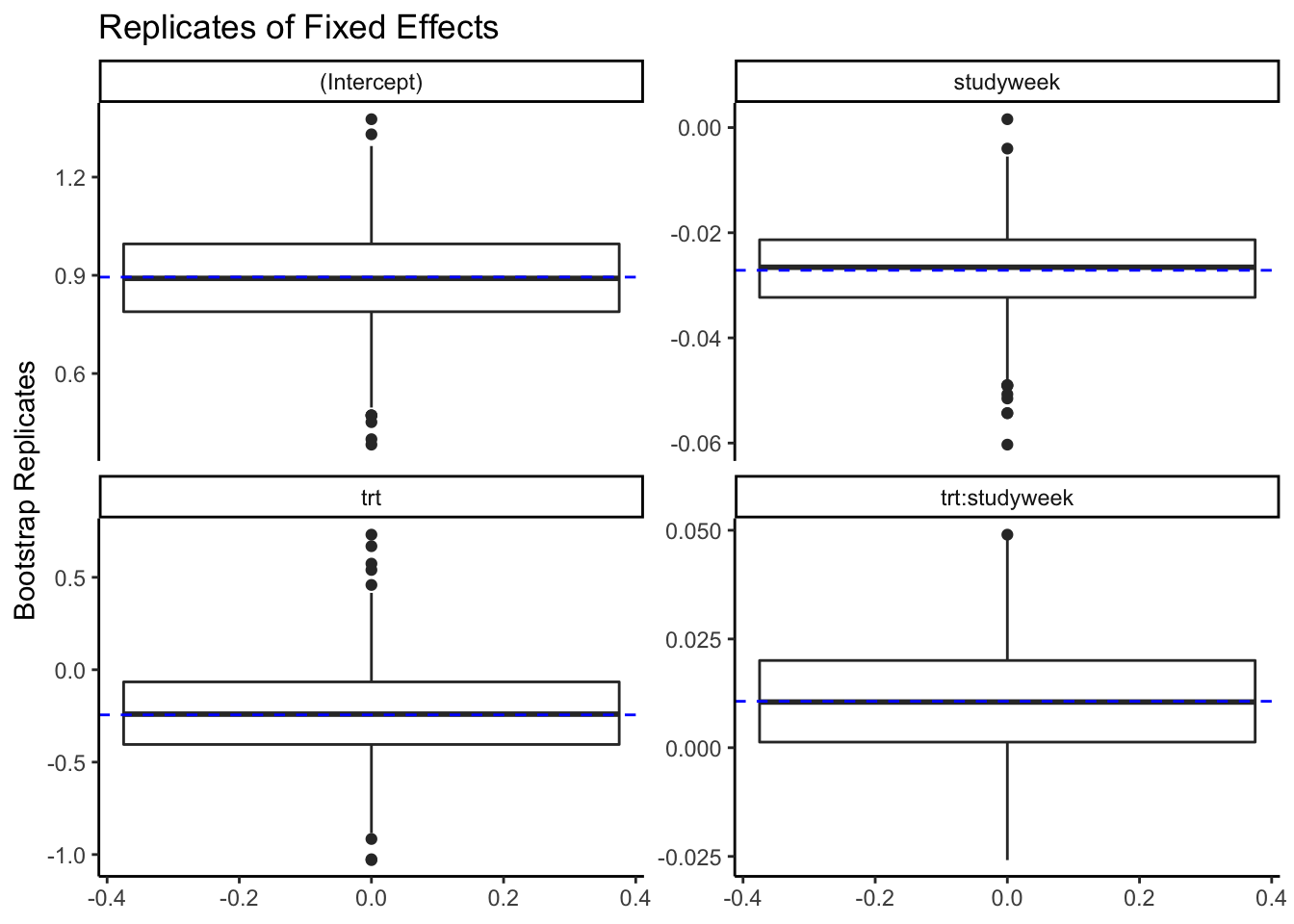

  • variances of random effects
plot(rwlb_reps, 
     parm_subset=c("s_1", "s_2", "rho")) + 
  ggtitle("Replicates of Variance Components")+
  theme_classic()

Bootstrap glmmBoot
Daniel Flores-Agreda
Daniel Flores-Agreda
Research Fellow (Biostatistics)

School of Public Health and Preventive Medicine of Monash University.

Related